Achieving Compressibility In Your Systems Mapping Practice

When mapping systems, achieving “compression” or “compressibility” in your maps is a best practice and a desirable skill. Compressibility is an indication of higher quality, more refined thinking. In other words, no matter how complex your map needs to be; if you can compress nodes in your map, it allows for you to see the 100,000 foot level; and then also have the ability to drill down to incredible levels of detail when needed for any node (sub-system) in the map.

The compressibility of a map refers to the ratio between total nodes (“boxes”) in a map to the total top level nodes. The higher the ratio, the more compressibility. For example, in the map below there are a total of 38 nodes and the number of top level nodes is 6 (three systems and three relationships), so the ratio is 6:38 or 1:9.5. This is a relatively high ratio. The map below is an example to show how compressibility works, but it is not uncommon for real-world maps to have dozens or hundreds of nodes. This can be overwhelming to both the map creator, and also can make communicating their understanding of the [mapped] system to others difficult.

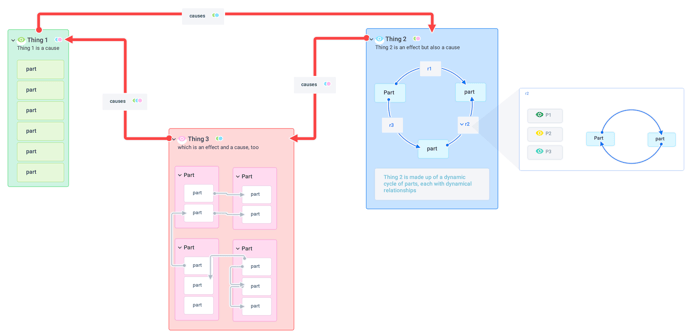
Example map uncompressed.

Example map compressed.

The individual who is trained in DSRP, will quickly notice that compression is a function of part-whole Systems (S) or the “S-rule.” So to increase the compressibility of your map do more part-whole work to “lump” various nodes into larger, nested groupings.

The system dynamics map below is an example of NON-compression or what might be called a “flat map” because there is no part-whole nesting. Thus, in this map there are 102 nodes and 102 top level nodes or a 1:1 ratio and therefore zero compression.  Maps such as this one are incredibly difficult for humans to understand which is likely why General McChrystal exclaimed, “When we understand that slide, we’ll have won the war.”

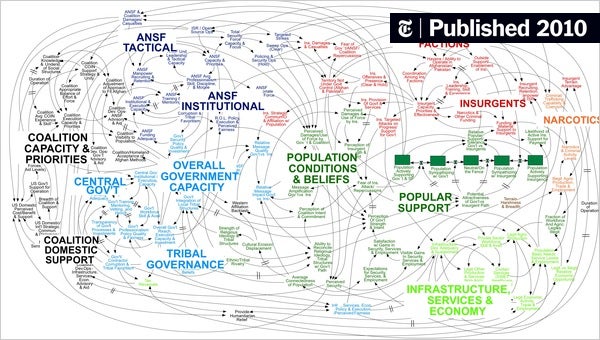Example System Dynamics Map

While there is no hard and fast rule on the optimal number of top level nodes, we do know that humans are capable of quickly grasping and “holding in their minds” 7 +/- 2 items. So we recommend that the number of top level nodes should be in this range.  Indeed, keeping the top level nodes within this range, the more total nodes a map contains the more compressibility the map exhibits. There is no limit to the nestedness and total number of nodes a map can contain, so compressibility is key to human understanding of large, complicated and complex systems.

Compressibility is a numbers game, but it is also a bit of art and science. Compressibility improves your maps and can lead to a better understanding of the system you are mapping and greater clarity in your thinking. In this way, a map with a large amount of detail and complexity can also be compressed to achieve underlying simplicity. Most problems we face, for example are easily reduced to simple jigs.

This simplicity can in turn be used to increase other people’s understanding of the system without needing to oversimplify the system (as one can always zoom in for greater detail).  In solving complex problems, this benefit alone is critically important, because getting everyone on the same page is half the battle.