Embrace And/Both Logic

This post is an excerpt from Chapter 7 of Systems Thinking Made Simple. 

A New Kind Of Logic

There is always an underlying logic implicit in both informal and formal systems thinking methods. Making the logic explicit leads to clarity of thought and deeper understanding of concepts. Logic is any system of principles that guides one’s thinking. It need not be formalized or even conscious. All of us use logic every day
without an awareness of what it is or where it came from. Systems thinking as a method also has an underlying logic.

The flaws of bivalent logic are pronounced as things get more complex, problems more wicked, and alignment with mental models more important.

Bi-valent vs. Multi-valent Logics 

Bivalent logic takes two values. The word comes from the combination of bi- (two) and -valent (being strong). So we can think of bivalent logic as having two strong positions: right or wrong, on or off, guilty or not guilty, true or false, 1 or
0. These are all forms of bivalent logic invented by Aristotle. This and another of Aristotle’s favorite logics, categories, is the basis for Western civilization.

It would be hard to overestimate the enormous impact that bivalent logic has had on society, both positive and negative. Bivalent logic is quick, easy, and clean. Unfortunately, in reality, nearly infinite shades of gray exist in between the logic of right and wrong, black and white, or even liberal and conservative. Bivalent logics lead to static and permanent ideas such as categories. You can’t sometimes belong to a category and sometimes not. In general, bivalent logic is like law and order, it's nice to have just the right amount of it, but too much is oppressive, controlling, and curbs liberty. Bivalent logic is also not how the real world works, which can be a significant downside when accuracy is important. That’s not to say that bivalent logic can’t approximate the real world, sometimes remarkably well, but the flaws of bivalent logic are pronounced as things get more complex, problems more wicked, and alignment with mental models more important.

Multivalent logic has more than two outcomes. It can be difficult, messy, and slow. It can take more time to consider the multiple options. Worst of all, you won’t ft in, because most people adhere pretty exclusively to the bivalent logic of their training. In contrast, if you’re in an environment where questioning assumptions and biases or thinking creatively or systemically about things is encouraged, then multivalent logic is a good route to take. But wait a minute! Isn’t contrasting these two forms of logic bivalent? Isn’t there a middle way?

The Power Of And/Both Logic

Maybe we "and/both" over "either-or." DSRP logic can be bivalent and multivalent? Let’s take a look at how it works. Let's choose the letter “A”. Let’s think of A as a variable for Anything. A can be anything you want it to be, including nothing at all. If you think of the letter A, you cannot think of it without all four DSRP patterns. Here’s why:

If you think the idea A, then you must also think of the idea “not-A” because A cannot exist devoid of context. Of course, this may be happening unconsciously. Let’s call A the thing and not-A the other. So far, so good—you’ve made a distinction between A and not-A.

Figure 7.1: Any Identity (A) Implies the Other (not-A)

A and not-A must be related because one literally implies the other.

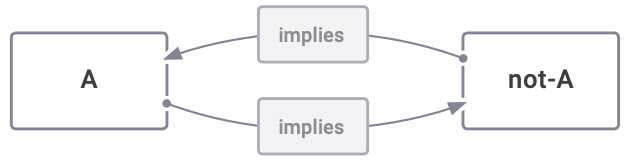Figure 7.2: A Relationship of Co-Implication Is Necessary

So far, we can see that even for a thing as simple as the letter A, we require two structures of thought: a distinction and a relationship. What else is implied?

The simplest kind of system can be defined as a relationship between a whole and its part or parts. A and Not-A are two parts related to one another, and thus comprise a system. Now we see that for the simple thought A to occur, we need to be able to create a thing-other distinction, a relationship, and a part-whole system.

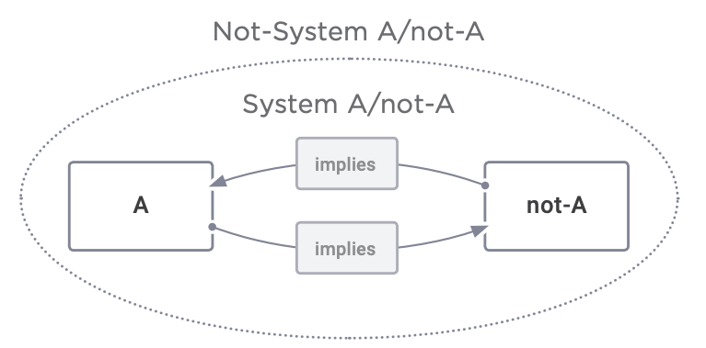Figure 7.3: When Any Two Things Are Related, a System is Formed (and a Not-System)

Notice, too, that the System A/not-A instantly implies a Not-System A/not-A. This is because as soon as you draw that circle around the system, you’re creating a new boundary or distinction: the system and the not-system.

Now, notice something interesting. Not-A was defined by A in the first place. It’s as if it didn’t have an identity separate from A. But the truth is that the other stuff that is not-A has its own identity independent of A. It’s just that because we’re focused on A, we’ve defined this other stuff in terms of A.

This whole idea of not-A is based on a perspective because not-A is defined in terms of A. So in the same way that we started with A, we could have just as easily started with not-A. You can imagine that not-A might have its own identity, such as “B.” We can see that even a simple idea like A or B requires a fourth element: perspective. Every perspective is made up of a point and a view.

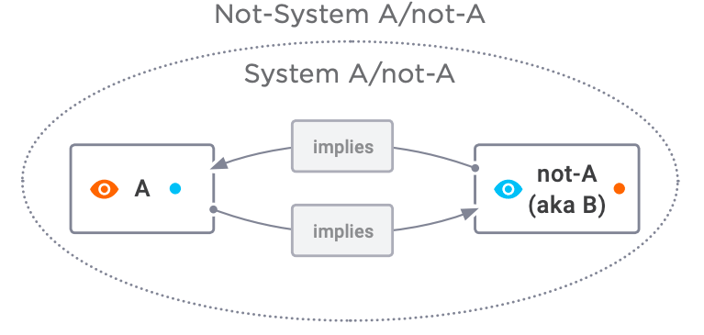Figure 7.4: Perspective Is Also Necessary, B in Terms of A, or A in Terms of B

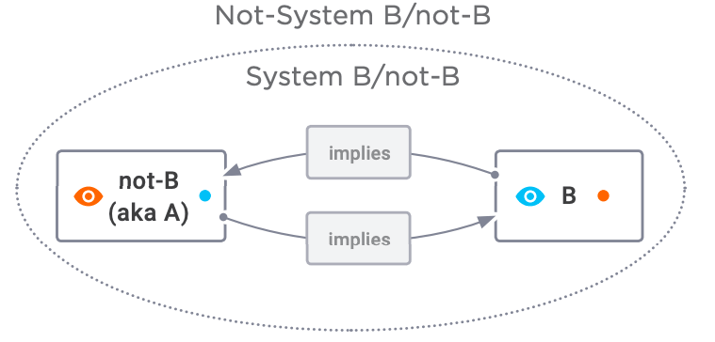Figure 7.4 (Continued): Perspective Is Also Necessary, B in Terms of A, or A in Terms of B

If you think this is just an academic point, consider how perspective logic is used to recast one’s political opponents in a negative light. Pro-life is recast as anti-feminist or anti-choice. Pro-choice is recast as pro-abortion or anti-life. There’s a reason why we don’t let our political opponents name us in terms of their position.

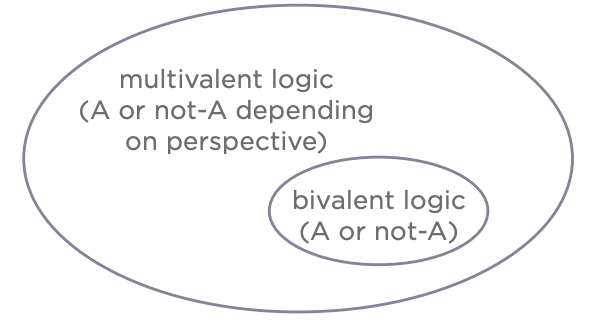Figure 7.5: Bivalency Inside of Multivalency

There you have it. In order to have any idea or thing, which we called A, you need to make a bivalent distinction between it and not-it. In doing so, you’ve made a relationship, part-whole systems, and taken a perspective. This means we start with a bivalent system (A/not-A) and then realize that our bivalent system is sitting inside a multivalent system. It means that A/not-A only has meaning from the perspective of A and that all of the other possible distinctions one could make also have perspective. Therefore, there are infinite shades of gray in between A and not-A, unless you ask from the perspective of A, and then there’s two. Bivalent logic is encapsulated in a multivalent system of logic.

Figure 7.6: Old Vs. New Logic

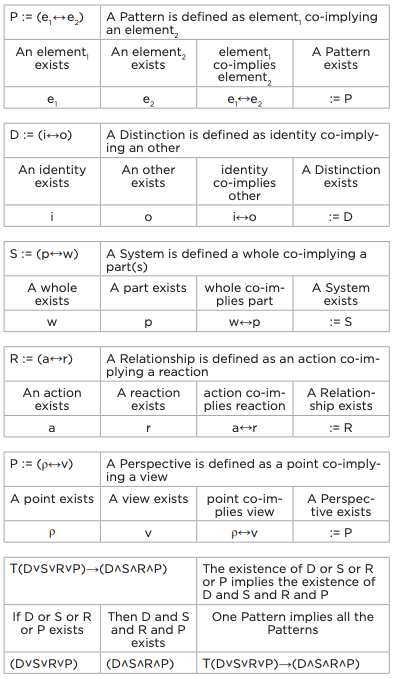Table 7.1: Underlying Multivalent Logic of DSRP