Network Theory
 Derek & Laura Cabrera
·
6 minute read
Derek & Laura Cabrera
·
6 minute read
This article is a part of our ongoing "System Models" series that looks at various systems models through the universal lens of DSRP in order to identify their strengths and weaknesses. Check out the system models tag here.
Excerpt from the book: Systems Thinking Made Simple, Chapter 8
Network theory is one of the most popular and powerful systems thinking methods. It is by far the most used, even if many of those who use it don’t think of it as systems thinking. Network thinking is a useful tool for thinking about systems of all kinds: physical, biological, chemical, ecological, neurological, psychological, social, economic, and so on. Let’s explore the basics of network theory in order to show how a few simple additions can dramatically and profoundly impact network theory as a whole while also improving systems thinking.
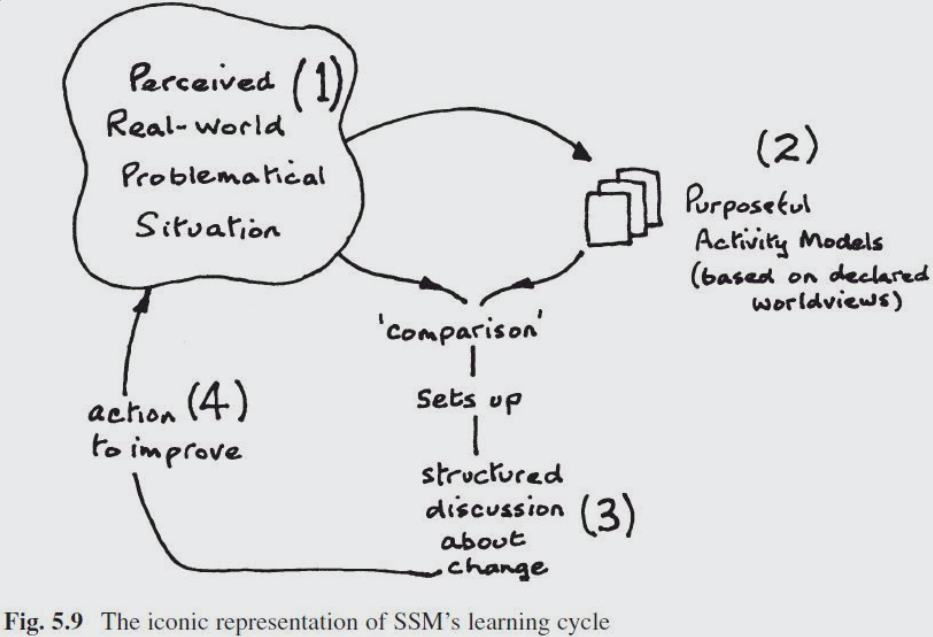
Remember that visualization is critically important for human understanding. Network theory has provided an interdisciplinary tool for understanding complex systems in a visual way. Networks consist of nodes and edges (See Figure 8.28).
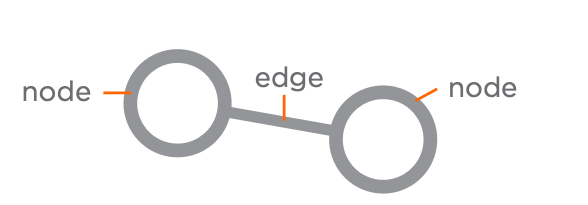
The world is teeming with complex interactions. From this simple everyday inter-activity emerge complex webs of relationships. Some of the most fascinating and challenging systems are simply the result of many interactions. In these systems, the ways in which people or things are connected can dramatically affect the properties of the emergent system or network. Yet despite all this complexity, the simple node-edge construction of networks provides us with one of the most powerful visual-mathematical abstractions we have, capable of capturing the complexities of many real-world phenomena. Some connections are very strong like the relationship between predator and prey, other less so. But in most systems the pathways of interaction are crucial to the system behavior. The specifics of who can interact with whom affect the properties of the system and its internal processes.
Network theory explains complex systems of interaction using the simple premise that their parts are often connected to each other. For example, a network of websites and hyperlinks forms the world wide web, a vast and complex information network that is the backbone of the information age. Predator-prey interactions form an ecological network called a food web, the circuit diagram of an ecosystem. Complicated networks of human interaction form dynamic social webs, which are woven into the fabric of society. Financial markets, disease, weather systems, biological and ecosystems, concepts, languages, and economies are all networks. Even humans are nothing more than systems of networks: circulatory, renal, respiratory, neural, conceptual, etc.
Complexity theory holds that simple rules and local interaction underly complexity. Networks follow this theory because the simple micro-level interactions between nodes “add up” to become the large-scale behavior of the system. We want to be able to predict how the system will behave based on the simple underlying interactions, such as who or what connects to whom, and how many connections exist between and among the nodes. We see similar behavior across wildly different types of network structures, despite different specifics. This means that much of the behavior we see is occurring because of the structural and dynamic properties of the network, whether the nodes involved are as diverse as events, people, ants, cars, genes, cells, or computers.
Extending network theory with DSRP
DSRP rules extend network theory in simple but profound ways. Some of these ways simply explicate ideas that are implicit in network theory already, whereas others add new structures and insights. In the text and figures that follow, we will walk you through the DSRP applications to network theory.
Start with a basic network of nodes and edges (See Figure 8.29). It could be any type of network, simple or complex. Think of this network as an abstract visual-mathematical representation for understanding systems.
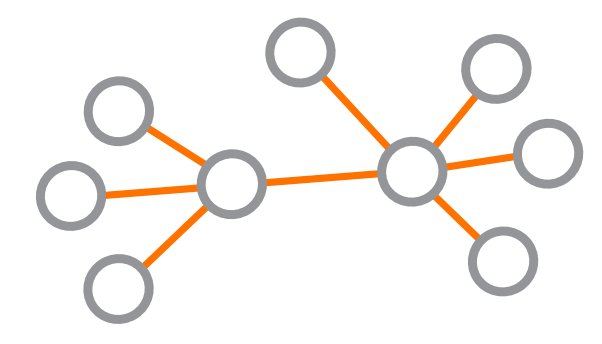
In Figure 8.30 we begin to extend basic network theory. Any node can be related to other nodes via edges (with or without directionality). But, by combining the distinction and relationship rules of DSRP, each of these edges could be its own node. Think for example of two computers linked together by a cord. Both computers are distinctly different things, but so is the cord itself.
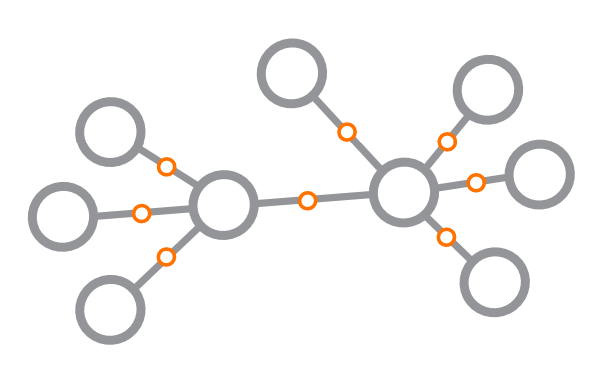
Figure 8.31 shows another important extension of network theory that is either implicit or nonexistent. Any node (including edge-nodes we created in Figure 8.30) can be a whole system made up of parts with equal, lesser, or greater complexity relative to the whole. This is implicit in network theory for nodes themselves, and explicit in terms of clustering. It is important to note that this can occur to any node, including edge-nodes. What this means is that every node (large or small) in Figure 8.31 has the potential to be a complex system made up of many related parts, and so on.
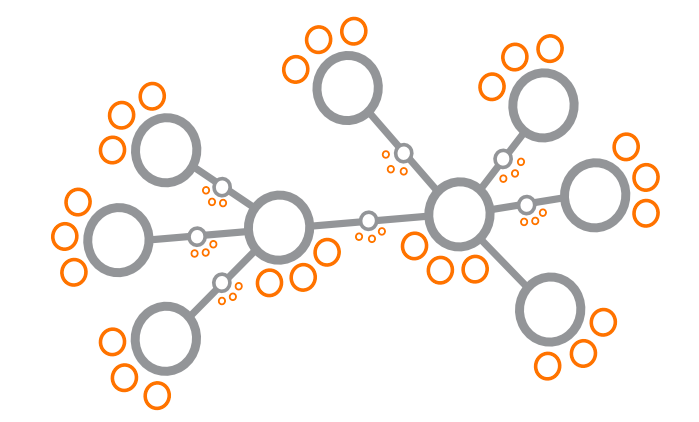
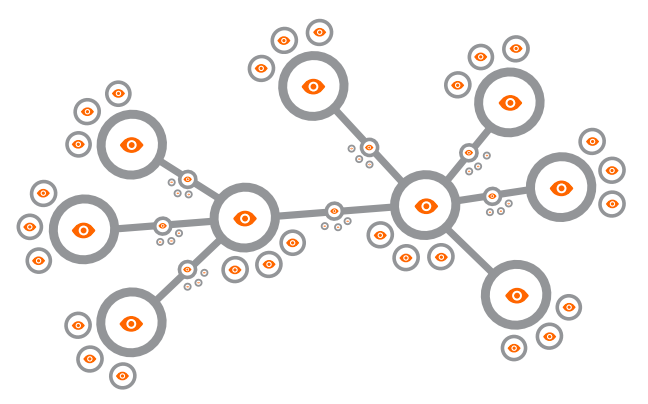
Any node (or system of nodes) can be the point or the view (eyeball) of a perspective. This means that every node in Figure 8.32 (which is everything) can be the point of a perspective, making all the other nodes the view. This is not explicit in network theory.
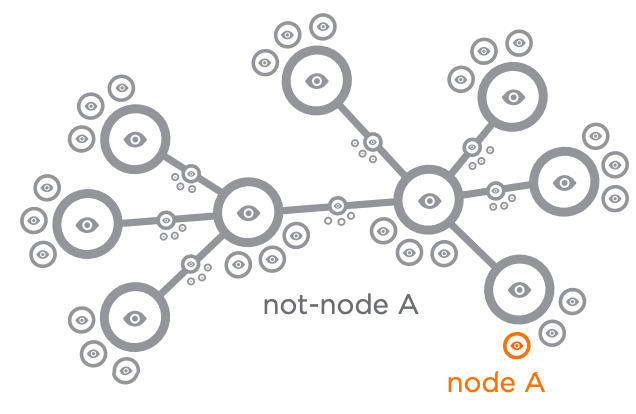
Every node is distinguished by the other nodes it is with. This is not explicit in existing network theory. Figure 8.33 shows that any node (an identity) is defined not only by what it is, but in contrast to system of things it is not (in red). This is a new insight (scale-free boundary conditions) that is often overlooked in network theory and essential to systems thinking.
If the DSRP rules were fully explicated on all nodes and edges of a network (as shown in Figures 8.29-8.33) the maximum potential complexity of the network would be reached. In other words, no matter how complex the system gets (in theory at least), we would have a conceptual model capable of capturing it.
Of course, in the same way that all nodes in a network do not need to be related (have an edge between them) even if they could be, not all the nodes in a system need to manifest every DSRP possibility. They are just representations of what is possible. In practice, all nodes, all edges, and all rules would require the power of a supercomputer and countless variables would remain unknown. Nonetheless, since DSRP rules elucidate what should exist structurally they have predictive power.
What would a network look like that has the extended properties we have outlined? Facebook. Because Facebook is a social network, it's easy to understand that it is perspectival. Each person's view of Facebook is unique. For example, when we all visit www.apple.com, we all see the same webpage. But when we point our browser to www.facebook.com, we all see a webpage that is from the unique perspective of our profile. So although our group of Facebook friends represents a traditional node-edge network, we can also see that every one of the nodes has a unique perspective on the network. None of the nodes (people) in the network are seeing a bird's eye view of the Facebook network, we are each seeing a tiny slice that includes the people we are connected to. We also can see that each profile is a rather large whole system made up of many parts that are stored in a large data table (all our friends, family, groups, pages, images, posts, shares, likes, etc.). There's also a less known feature in Facebook called relationships. You can go to any friend's profile page and click on the top right to "see relationship." This allows you to see a uniquely generated page that represents the relationship between you and your friend. It combines all the parts that you share into a distinct page. This relationship page has a unique identity and a unique URL that combines the names of you and your friend. This means that the relationship is a distinction but it is also a system.
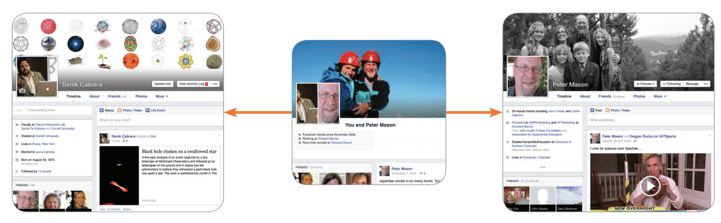
You can see this in Figure 8.34, which shows the relationship between Derek and one of his old climbing buddies, Peter. On the left is Derek's profile page; on the right is Peter's. In the middle is the relationship between Derek and Peter (from the perspective of Facebook!), which includes all of the parts of their relationship: comments, things they've both shared, photographs from past climbing expeditions, and mutual friends and workplaces. What we can see is that Facebook is a network that is based on distinctions (every identity is different and contrasted with others), systems (every profile is a system made up of many parts), relationships (shared items and interactions between profiles, likes, comments, etc.), and perspectives (every profile is a unique perspective on the system).
It is easy to see this on Facebook, because it's a social network where all the people have eyes and brains. But can we see that the same dynamics are at play in an ecological web? Do we grasp that the same underlying structure and dynamics are true for a computer network, a gene network, an author citation network? Or that each organism, computer, gene, or cell experiences the ecosystem from their unique perspective and makes decisions, builds relationships, and behaves based on this perspective? Can we see that within each interaction between any two things is an entire world of complexity? Do we understand that even for inanimate things like ideas, atoms, and words, our mind utilizes perspective to understand?
When we understand that everything can be imagined in terms of networks, that's a big step. But when we see that any system can be thought of in terms of networks following DSRP rules that's quite profound. Nothing can get more complex than a network of individual nodes that are co-defining each other, relating and not relating to each other, assembling into and out of part-whole groupings, and taking perspectives on slices of the whole. When we take into account that, like Facebook, every relationship has the potential to also be a distinction and a system capable of containing immense complexity, our thinking aligns with the way the world actually works. Complex? Yes. But simple underneath.
Check out our 4 part series on network theory developed at the Santa Fe Institute.
.png?width=150&height=150&name=CRL%20GOAT%20Logo%20(4).png)