·
3 minute read
This blog was written by Patrick Kastner as a project for PADM 5449 at Cornell University.
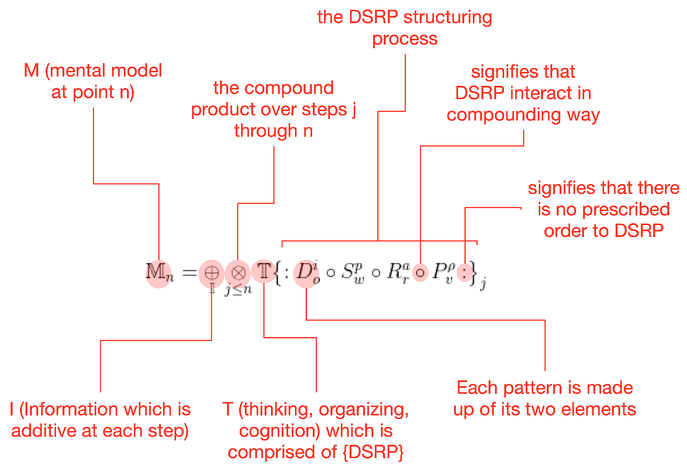
Making decisions is part of our everyday life. While decision making with finite options may seem straight-forward, the complexity in policy-related contexts grows significantly due to the number of alternatives either being infinite and not countable or very large if countable. Moreover, in these contexts, the alternatives themselves are not explicitly known. This essay aims to shed light on why decision making for multi-stakeholder problems is difficult and provides a mental model that, if applied, allows for better outcomes. For this, we leverage the concept of cognitive sliders—content-related mental models that apply to a wide array of situations or circumstances (Cabrera, 2020).
When discussing the decision-making process, it is helpful to deconstruct decision making into its constituent parts: processes, criteria, and outcomes, see Fig. 1. The objectives are criteria used to evaluate our options. Different individuals may have personal preferences about which objectives are important to us as stakeholders in the decision-making process. During decision making, the decision-maker (DM) engages in a search or search-for-alternatives process and a decision process. The search and decision processes are constrained and affected by the objectives and individual preferences, respectively. Both the search and decision processes are intertwined and ultimately lead to an outcome: the solution. Good decision making, arguably, would be to reach a solution that meets the individual preferences of all of our stakeholders.
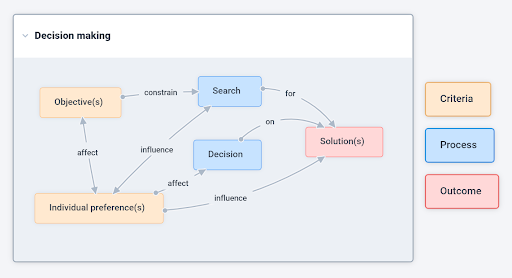
Fig. 1: Part-whole structure of decision making.
Both in personal and professional settings, we often deal with multiple stakeholders, each with their individual preferences, that may not be in agreement with each other. This begs the question, which aggregation procedures exist to consolidate many individual preferences into one preference preferred by everyone? To achieve that, we need to find a way to evaluate each of our objectives in a methodical way to determine an evaluation score for each alternative. The simplest way would be to ask each stakeholder to rank-order all alternatives according to their individual preference, and to evaluate the result with a pairwise majority decision, see Fig. 2. “Decide, then search”, short for the elicitation of individual preferences before searching, for a solution is called a priori preference articulation.
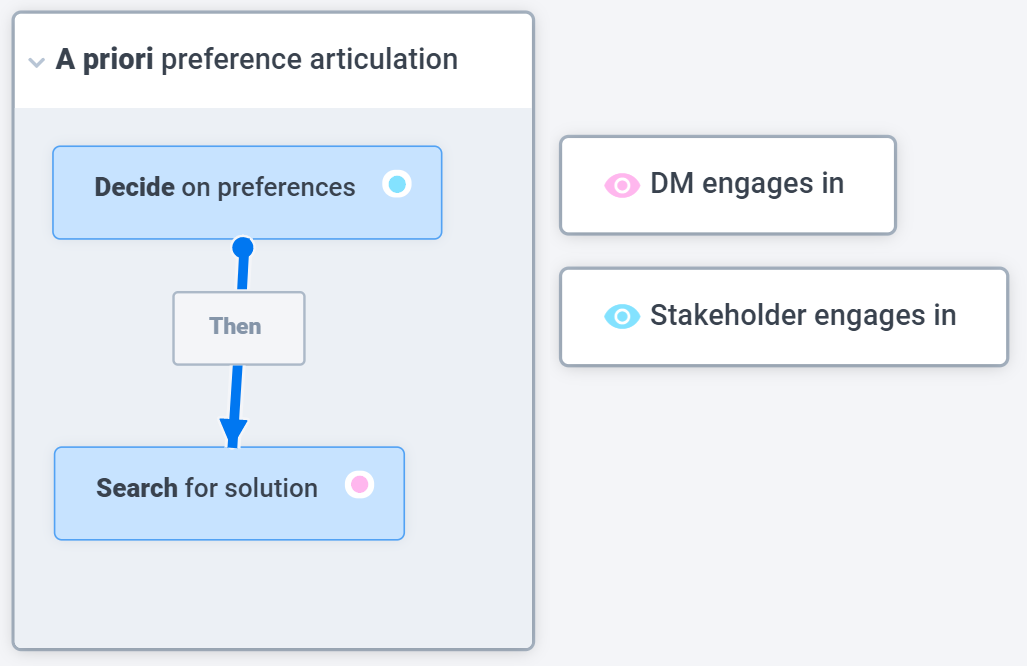
Fig. 2: The decision-making process with a priori preference articulation.
The example above is called the “paradox of voting” and was discovered by Marquis de Condorcet (1785). Kenneth Arrow (1950) built on this idea in his famous “Impossibility Theorem” about collective decision making. Suppose there are alternatives to choose from in a decision-making context such as a new office, public policies, or just about anything else. According to Kenneth Arrow, it is impossible to translate the preferences of multiple stakeholders into a coherent public policy that is consistent with the expressed preferences of all individuals. It follows that the aggregation of preferences across multiple individuals will always favor some individuals over others. Furthermore, not only will it always favor some individuals over others, but it is also difficult for the DMs to ascertain, a priori, the extent to which this effect happens, yielding the potential for severe opportunity costs.
Some decades later, the engineering community established that Arrow’s theorem not only applies to social choice problems but also to multi-criteria design problems (Franssen, 2005), categorizing social choice and a large subset of engineering problems as formally equivalent. “Search, then decide”, a novel, so-called a posteriori preference articulation approach has been suggested (Veldhuizen & Lamont, 2000) and shown to be superior to the a priori approach (Singh et al., 2015) in an attempt to remedy the costly unintended consequences of unknowingly favoring some objectives over others.
Structurally, we see that both approaches are composed of a temporal relationship between the search process and the decision process, see Fig 3. The a posteriori approach implements an additional feedback loop that lets the DM re-engage in the search for optimal solutions of the stakeholders to change their opinion about their preferences during trade-off analysis.
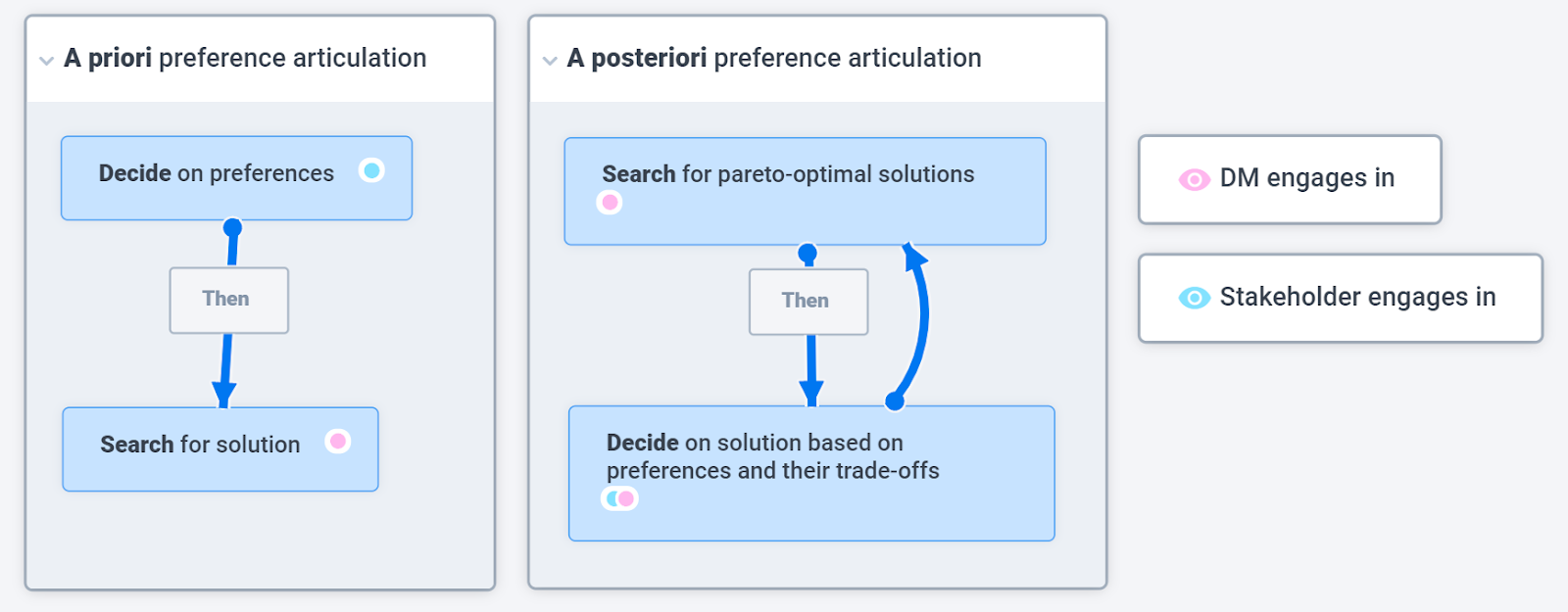
Fig. 3: Decision-making process with a priori vs. a posteriori preference articulation.
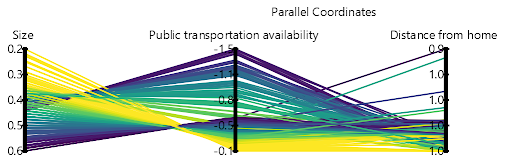
The a posteriori approach can informally be described as “choosing what I prefer once I know what I can get”. Here, each stakeholder is tasked with identifying the minimum threshold that they are willing to accept for each objective after the search for (Pareto-optimal) solutions has been completed. The result would be all feasible solutions, represented as lines in the parallel axis plot in Fig 4 (b). Now, because the individual preferences are elicited after the search, stakeholders have an immediate understanding of the consequences of their preferences and their sensitivity during trade-off analysis. At this point, if very few or none of the office space candidates are found to be attainable, the stakeholders can be asked to either alter their thresholds or to add/remove objectives and to re-engage in trade-off analysis after another search has been performed.
(a) After search: all possible office space candidates
(b) During trade-off analysis: all feasible office space candidates.
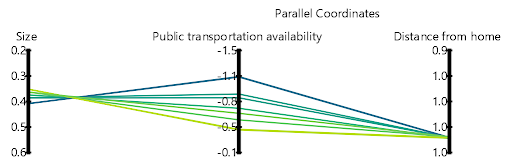Fig. 4: Trade-off analysis for decision making problem. In this hypothetical example, every line represents one office space candidate.
References
