·
2 minute read
Over the years, different variables/symbols have been used for the same equation. In some cases for good reason, and in other cases solely because, like an English sentence, a mathematical sentence can be read and written in different ways toward the same effect. For example, take the following four equations:
M=I+T
K=I+T
m=i+t
k= i+t
You can think of all four of these as synonymous equations. The reason for their superficial difference is many-fold. First, sometimes it's easier to not use the capital letters (so general laziness). But the capitals are the correct version, but only because the letter "i" will get confused as a variable with the letter used for identity (i). But when we use the capital letter M this can be confused with the variable for Mission in VMCL which is also M. So, the best case scenario is to use the double stroke letters as in:
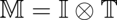
However, it is sometimes difficult without a math program to write the double-stroke letters so single stroke will do. You can see in the table below we use simple capital letters because it would take a bit more work to insert double-stroke capital letters as small inline images.
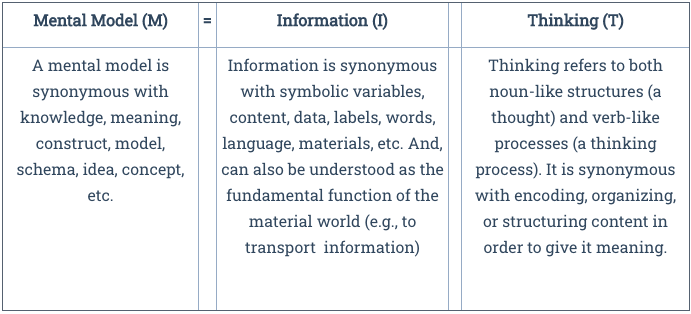Table 1: Mental Models
What is far more important is that you understand what the equation means and why certain terms like "knowledge" (k or K) are interchangeable with mental models (m or M). In school settings, for example, the term mental model is not used (unfortunately) as much as the term knowledge. Thus, we will often use the K=I+T variant of the formula. In addition, in some cases we have used the lower case "k" to represent an individual's knowledge versus the upper case "K" as the knowledge of society writ large (same for m and M). Knowledge and mental models are the same thing—they are synonyms—because knowledge is what happens when information gets organizes to form meaning. The same is true of mental models. Mental model (or schema) is a term that scientists use and knowledge is a term the general public uses. But there is great confusion around what knowledge is and how it is formed. So, we sometimes try to push the general public to use terms like mental models to be more accurate. As a term, "Knowledge" has many preconceived biases and pitfalls associated with it (for example, that knowledge is the same as fact, or that only experts create knowledge, or that only science creates knowledge)
Now let's deal with the relational symbol (the operator) in between I and T. It is sometimes written as a "+" and sometimes a "x" and sometimes a "⊗" or "compound product." This is because, in the formal equation for DSRP (which makes up the T) is written thus:
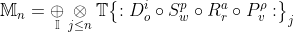
This equation might look a bit daunting, but if you break down what it is saying, it is not too bad. It basically describes how the creation of mental models is a complex adaptive system where informational agents (I) follow simple rules recursively until some stopping point (which is also defined by the simple rules). The simple rules are DSRP and these act on information. Below the formula is broken down:
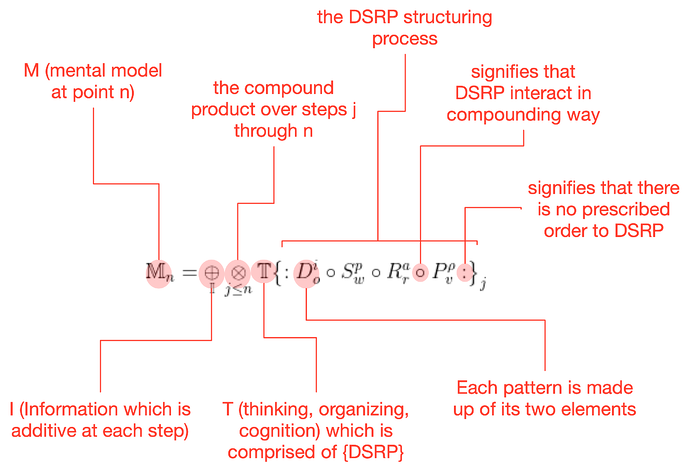This in turn gets shortened to:
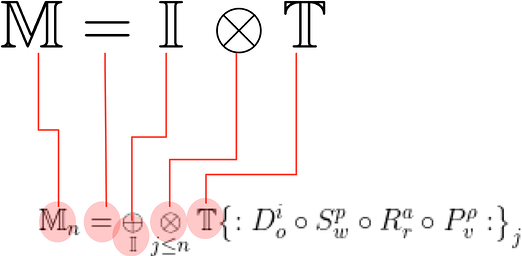
What you can see from this is that the "operator" between I and T is a bit more complex than "+" or "x" because it is compounding and recursive as well as being simultaneously additive (in terms of information). So, where "+" is sometimes used to simplify the equation (as in M=I+T), it is really a bit more accurate to say M=I⊗T. However, even this is not entirely accurate but a form of shorthand and the symbol ⊗ is not only sometimes hard to find and use electronically but is also not understood by many folks. Thus, especially in school settings with younger children, we use the simplification M=I+T. We avoid using the simplification M=IxT because it begs the question whether T=M/I which is not necessarily true.
